Aditya Bisht's Blog

Algorithms : Finding Connected Components in a Graph

Aditya Bisht's photo
Aditya Bisht
·

3 min read

Overview

In a graph, all nodes might not be connected with each other. Let's take an example of a graph with 5 nodes-

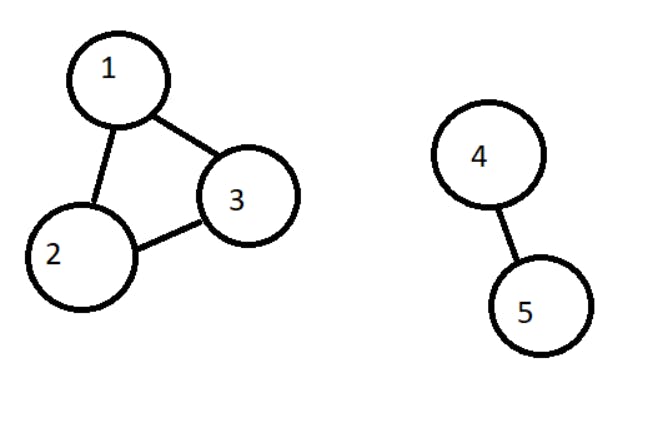
Here you can see that 1-2-3 are connected and 4-5 are connected. Here , 1-2-3 is called one connected component.

How to determine if a connected component is present ?

  1. Start a BFS or DFS from any node of the graph.

  2. If you are able to visit all the other nodes from that single node that means the all nodes in the graph are connected.

  3. If you are unable to reach a particular node or a group of nodes, then that group of nodes might be a different connected component.

How to find connected components?

  1. Let's take an adjacency list based graph.

  2. Traverse the adjacency list and for every node do a BFS or DFS on the node and mark all the nodes you visit in this way as visited.

  3. While traversing the list do not do BFS on the nodes which have already been visited.

  4. Hence everytime you do a BFS/DFS you are traversing a connected component so you can count the number of times you do a BFS/DFS.

Let's understand with the help of an example:

Leetcode 0547- Number of Provinces

There are n cities. Some of them are connected, while some are not. If city a is connected directly with city b, and city b is connected directly with city c, then city a is connected indirectly with city c.

A province is a group of directly or indirectly connected cities and no other cities outside of the group.

You are given an n x n matrix isConnected where isConnected[i][j] = 1 if the ith city and the jth city are directly connected, and isConnected[i][j] = 0 otherwise.

Return the total number of provinces.

Here, the given graph is in the form of an adjacency list. When we perform bfs/dfs starting from one particular node, we get one connected component. To make sure we get all connected components we need to traverse the adjacency list and make sure all nodes have been visited.

The following is the solution to the leetcode question given above. I am using breadth first search to traverse a single component.

class Solution {
  public void bfs(int isConnected[][],int visited[],int node){

        Queue<Integer> q=new LinkedList<>();
        q.offer(node);

        while(!q.isEmpty()){
            int current=q.poll();
            visited[current]=1;

           for(int i=0;i<isConnected[0].length;i++){
               if(isConnected[current][i]!=0 && visited[i]!=1){
                   q.offer(i);
                   visited[i]=1;
               }
           }
        }


    }

    public int findCircleNum(int[][] isConnected) {

        int i,j,provincecount=0;
        int visited[]=new int[isConnected.length];


        //traverse through the adjacency array
        for(i=0;i<isConnected.length;i++){

            if(visited[i]==1){
                continue;
            }
            for(j=0;j<isConnected[0].length;j++){

                //if not visited and is connected
                if(visited[j]==0 && isConnected[i][j]==1){
                    //everytime u do a bfs u complete one connected component
                     bfs(isConnected,visited,j);
                    provincecount++;
                }

            }
        }

        return provincecount;
    }
}
DSAgraphs